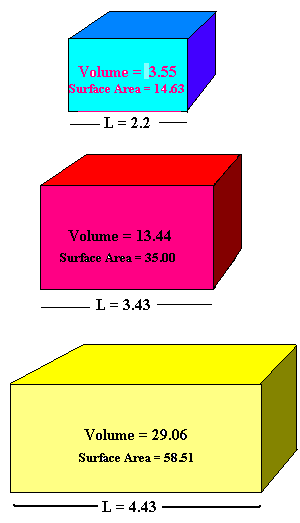
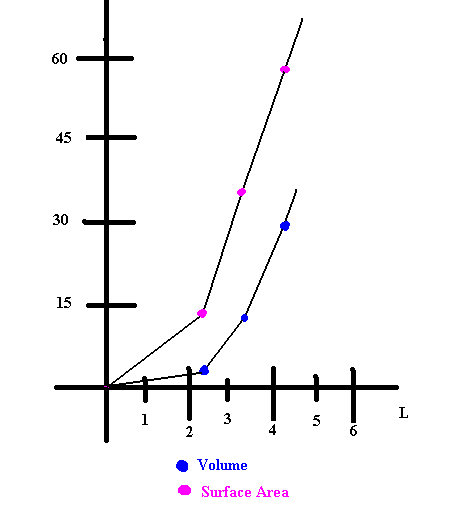
Side Length, Volume, and Surface Area of Similar Solids.
The two-part example below illustrates how you can learn about the length, perimeter, area, and volume of similar objects.. In the first part, you can see that the side lengths of three similar rectangles and the scale factor, perimeters, and areas of the two rectangles are related.
Your task is to investigate how changing the lengths of the sides of a rectangular prism affects the volume and surface area of the prism. First notice that the three rectangular prisms are congruent (equal angles and equal sides). Then look at the graph depicting the rate by which volume and surface area increases in response to the change of perimeter.


As you experiment with different ratios of side lengths (different scale factors), you can also observe the changes in the volume and surface-area data.
You may notice a difference in the appearance of the graphs. It is important to focus on why the relationship between side length and volume is cubic whereas the relationship between side length and surface area is quadratic. It contributes to students' understanding of the measures of length, surface area, and volume.
Task
How are the perimeters,
areas, and side lengths of similar rectangles related? Imagine that all three
rectangles above the same one, stretched out. By changing the size and
shape of the blue rectangle (into red and yellow) we notice that the red and
yellow rectangles remain similar (congruent
angles, proportional sides). If we were to change the scale factor,
the proportions would remain the same as well.
Volume
In order to find volume, we must not only multiply the length x width, but now we must take into account the object's depth. What is depth? Take for instance this cube with a depth of 6 units.
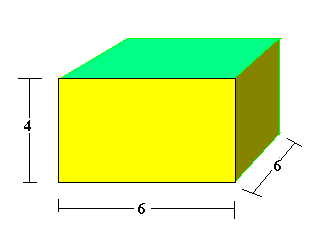
The Volume is length x width, or (area) x depth. If we know that the surface of the 2-dimensional triangle is 6cm x 4 cm, then it must follow that taking this same equation 6 times will cover the area of the entire figure. See the figure below for a demonstration of depth.

Volume = 4 cm x 6 cm x 6 cm.
Don't forget to multiply the cm too!
Volume = 24 square cm x 6
Volume = 144 cubic cm.
Surface Area
As we saw above, the surface area is directly related to the volume. In order to find the surface area we must now add all (area) sides of the figure, excluding the insides of the cube. Pretend it is a hollow. We are looking at surface planes:
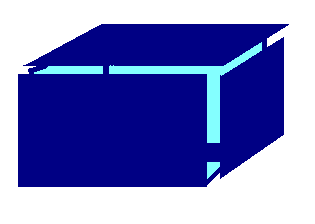
Therefore, when we calculate the surface area, we must take the area of EACH side and add it together. NOTE: You will have to sketch your own cube in order to see all the sides of the rectangle! See sketch below:
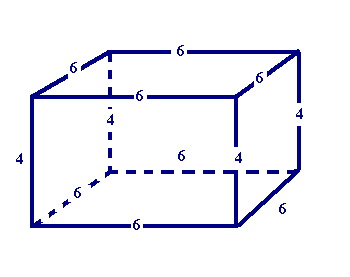
The surface area is going to be Area of Side 1 + Side 2 + Side 3 + Side 4 + Side 5 + Side 6
(6 x 4) + (6 x 4) + (6 x 4) + (6 x 4) + (6 x 6) + (6 x 6) = 24 + 24 + 24 + 24 +36 + 36 = 168 square units
Now let's try some practice problems! GOOD LUCK!!